Question

Solve for $x$, where $x > 0$ and $0 = -21x^2 - 11x + 40.$ Express your answer as a simplified common fraction.
`Solve for $x$, where $x \ \textgreater \ 0$ and $0 = -21x^2 - 11x + 40.$ Express your answer as a simplified common fraction.`

Answer 1

`\large \boxed{\sf \ \ (8)/(7) \ \ }`

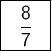
Explanation:

Hello, please consider the following.

The solutions are, for a positive discriminant:

`(-b\pm√(\Delta))/(2a) \ \text{ where } \Delta=b^2-4ac`

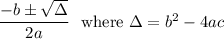
Here, we have a = -21, b = -11, c = 40, so it gives:

`\Delta =b^2-4ac=11^2+4*21*40=121+3360=3481=59^2`

So, we have two solutions:

`x_1=(11-59)/(-42)=(48)/(42)=(6*8)/(6*7)=(8)/(7) \\\\x_2=(11+59)/(-42)=(70)/(-42)=-(14*5)/(14*3)=-(5)/(3)`

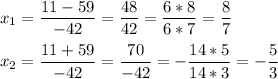
We only want x > 0 so the solution is

`(8)/(7)`

Hope this helps.

Do not hesitate if you need further explanation.

Thank you