Answer: 0.0899.
Explanation:
Given: CNNBC recently reported that the mean annual cost of auto insurance is 1048 dollars, the standard deviation is 282 dollars.
Sample size : n= 55
Let
 be the sample mean.
be the sample mean.
The probability that a sample of size n =55 is randomly selected with a mean less than 997 dollars:
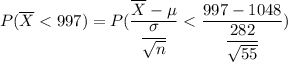
![=P(Z<-1.3412)\ \ \ [Z=\frac{\overline{X}-\mu}{(\sigma)/(√(n))}]\\\\=1-P(Z<1.3412)\\\\=1-0.9101\ \ \ \ [\text{By z-table}]\\\\ =0.0899](https://img.qammunity.org/2021/formulas/mathematics/college/juprphltyb272s15l9ci2dfaq01r9bwxo7.png)
Hence, the required probability = 0.0899 .