Question

The population of Adamsville grew from 6000 to 13000 in 7 years. Assuming uninhibited exponential growth, what is the expected population in an additional 3 years?

Answer 1

18107.32

Explanation:

Set up the exponential function in the form:

`P = P_0(R)^t`

so P is the new population,
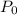`P_0` is the original population, R is the rate of increase in population, and t is the time in years.

You have to use the information given to find the rate that the population is increasing and then use that rate to find the new population after more time passes.

`13000 = 6000(R)^7\\\\\\frac{13000}{6000} = R^7\\\\\sqrt[7]{(13000)/(6000) } = R\\\\\\ R = 1.116786872`

Now that you found the rate, you can use the function to find the population after another 3 years.

`P = 13000(1.116786872)^3\\P = 18107.32317\\`

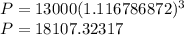
So the population is 18107, rounded to the nearest whole number.