Question

A student is given that point P(a, b) lies on the terminal ray of angle Theta, which is between StartFraction 3 pi Over 2 EndFraction radians and 2Pi radians. The student uses the steps below to find cos Theta. Which of the following explains whether the student is correct? The student made an error in step 3 because a is positive in Quadrant IV; therefore, cosine theta = StartFraction a Over StartRoot a squared + b squared EndRoot EndFraction = StartFraction a StartRoot a squared + b squared EndRoot Over a squared + b squared EndFraction. The student made an error in step 3 because cosine theta = StartFraction negative b Over StartRoot a squared + b squared EndRoot EndFraction = Negative StartFraction b StartRoot a squared + b squared EndRoot Over a squared + b squared EndFraction. The student made an error in step 2 because r is negative in Quadrant IV; therefore, r = Negative StartRoot a squared + b squared EndRoot. The student made an error in step 2 because using the Pythagorean theorem gives r = plus-or-minus StartRoot (a squared) minus (b squared) EndRoot = StartRoot a squared minus b squared EndRoot.

Answer 1

A.

The student made an error in step 3 because a is positive in Quadrant IV; therefore,

`cos\theta = (a√(a^2 + b^2))/(a^2 + b^2)`

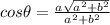
Explanation:

Given

`P\ (a,b)`

`r = \± √((a)^2 + (b)^2)`

`cos\theta = (-a)/(√(a^2 + b^2)) = -(√(a^2 + b^2))/(a^2 + b^2)`

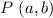
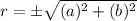
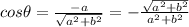
Required

Where and which error did the student make

Given that the angle is in the 4th quadrant;

The value of r is positive, a is positive but b is negative;

Hence;

`r = √((a)^2 + (b)^2)`

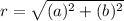
Since a belongs to the x axis and b belongs to the y axis;

`cos\theta` is calculated as thus

`cos\theta = (a)/(r)`

Substitute
`r = √((a)^2 + (b)^2)`

`cos\theta = (a)/(√((a)^2 + (b)^2))`

`cos\theta = (a)/(√(a^2 + b^2))`

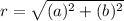
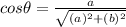
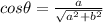
Rationalize the denominator

`cos\theta = (a)/(√(a^2 + b^2)) * (√(a^2 + b^2))/(√(a^2 + b^2))`

`cos\theta = (a√(a^2 + b^2))/(a^2 + b^2)`

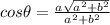
So, from the list of given options;

The student's mistake is that a is positive in quadrant iv and his error is in step 3