Answer:
Option (2)
Explanation:
In this question we have to find the values of Sinθ and tanθ where
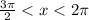 .
.
Cosθ =
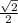 ⇒ θ =
⇒ θ =
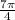
[Since
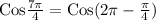
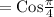
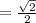 ]
]
Since Cosine of any angle between
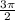 and 2π is positive and Sine is negative in nature,
and 2π is positive and Sine is negative in nature,
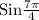 =
=
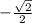
Since, tanθ =
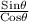
tanθ =
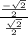
=
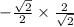
= -1
Therefore, Option (2) will be the answer.