Question

Cos(0)=√2/2, and 3π/2<0<2π, evaluate sin(0) and tan(0). Sin(0)?

Answer 1

Explanation:

option 2 is the correct answer

Answer 2

Option (2)

Explanation:

In this question we have to find the values of Sinθ and tanθ where
`(3\pi)/(2)<x<2\pi`.

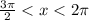Cosθ =
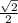`(√(2))/(2)` ⇒ θ =
`(7\pi )/(4)`

[Since
`\text{Cos}(7\pi )/(4)=\text{Cos}(2\pi-(\pi)/(4))`

`=\text{Cos}(\pi )/(4)`

`=(√(2) )/(2)` ]

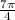
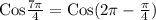
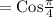
Since Cosine of any angle between
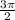`(3\pi)/(2)` and 2π is positive and Sine is negative in nature,

`\text{Sin}(7\pi )/(4)` =
`-(√(2))/(2)`

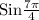Since, tanθ =
`\frac{\text{Sin}\theta}{\text{Cos}\theta}`

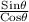
tanθ =
`((-√(2) )/(2) )/((√(2) )/(2) )`

=
`-(√(2))/(2)* (2)/(√(2))`

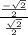
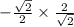
= -1

Therefore, Option (2) will be the answer.