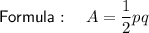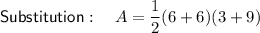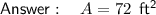Answer:
Formulas Used

where:
- a and b are the bases (parallel sides)
- h is the height (perpendicular to the parallel sides)

where:
- a and b are the legs of the right triangle
- c is the hypotenuse (longest side, opposite the right angle)

where:
- p and q are the diagonals
-----------------------------------------------------------------------------------------
Question g (Trapezoid)
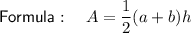
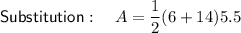
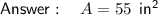
Question h (Trapezoid)
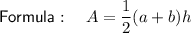
Find the missing side length of the right triangle using Pythagoras' Theorem:
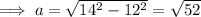
Therefore, top edge of trapezoid = √52 + 8
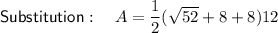
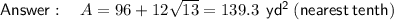
Question i (Kite)