Question

A team of four boys and five girls is to be chosen from a group of six boys and eight girls. How many different teams are possible?​

Answer 1

There are a total of 840 possible different teams

Explanation:

Given

Number of boys = 6

Number of girls = 8

Required

How many ways can 4 boys and 5 girls be chosen

The keyword in the question is chosen;

This implies that, we're dealing with combination

And since there's no condition attached to the selection;

The boys can be chosen in
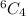`^6C_4` ways

The girls can be chosen in
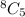`^8C_5` ways

Hence;

`Total\ Selection = ^6C_4 * ^8C_5`

Using the combination formula;

`^nCr = (n!)/((n-r)!r!)`

The expression becomes

`Total\ Selection = (6!)/((6-4)!4!) * (8!)/((8-5)!5!)`

`Total\ Selection = (6!)/(2!4!) * (8!)/(3!5!)`

`Total\ Selection = (6 * 5* 4!)/(2!4!) * (8 * 7 * 6 * 5!)/(3!5!)`

`Total\ Selection = (6 * 5)/(2!) * (8 * 7 * 6)/(3!)`

`Total\ Selection = (6 * 5)/(2*1) * (8 * 7 * 6)/(3*2*1)`

`Total\ Selection = (30)/(2) * (336)/(6)`

`Total\ Selection =15 * 56`

`Total\ Selection =840`

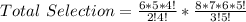
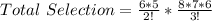
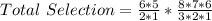
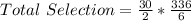
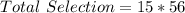
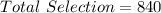
Hence, there are a total of 840 possible different teams