Question

PLEASE HELP WILL GIVE EVERYTHING Amare wants to ride a Ferris wheel that sits four meters above the ground and has a diameter of 50 meters. It takes six minutes to do three revolutions on the Ferris wheel. Complete the function, h(t), which models Amare's height above the ground, in meters, as a function of time, t, in minutes. Assume he enters the ride at the low point when t = 0.

Answer 1

`h(t)=-25\cos(\pi t)+29`

Explanation:

First thing to understand is that we will be producing a sine or cosine function to solve this one. I'll use a cosine function for the sake of the problem, since it's most easily represented by a cosine wave flipped over. If you're interested in seeing a visualization of how a circle's height converts to one of these waves, you may find the Better Explained article Intuitive Understanding of Sine Waves helpful.

Now let's get started on the problem. Cosine functions generally take the form

`y=a\cos(b(x-c))+d`

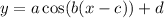
Where:

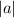`|a|` is the amplitude

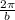`(2\pi)/(b)` is the period, or the time it takes to go one full rotation around the circle (ferris wheel)

`c` is the horizontal displacement

`d` is the vertical shift

Step one, find the period of the function. To do this, we know that it takes six minutes to do three revolutions on the ferris wheel, so it takes 2 minutes to do one full revolution. Now, let's find
`b` to put into our function:

`(2\pi)/(b)=2`

`2\pi=2b`

`\pi=b`

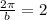
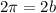
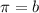
I skipped some of the basic algebra to shorten the solution, but we have found our b. Next, we'll get the amplitude of the wave by using the maximum and minimum height of the wheel. Remember, it's 4 meters at its lowest point, meaning its highest point is 54 meters in the air rather than 50. Using the formula for amplitude:

`(\max-\min)/(2)`

`(54-4)/(2)`

`(50)/(2)=25=a`

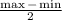
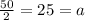
Our vertical transformation is given by
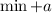`\min+a` or
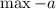`\max-a`, which is the height of the center of the ferris wheel,
`4+25=29=d`

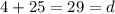
Because cosine starts at the minimum,
`c=0`.

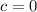The last thing to point out is that a cosine wave starts at its maximum. For that reason, we need to flip the entire function by making the amplitude negative in our final equation. Therefore our equation ends up being:

`h(t)=-25\cos(\pi t)+29`