Answer:
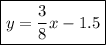
Explanation:
Part 1: Determining slope from two given points
We are given the points
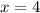 and
and
 . We can go ahead and make the first part of the equation because we are given one of the unknowns (the y-intercept, or
. We can go ahead and make the first part of the equation because we are given one of the unknowns (the y-intercept, or
 ). The equation becomes
). The equation becomes
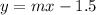 .
.
Part 2: Determine the coordinate points
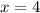 is a x-intercept, meaning it crosses the x-axis at this point. The y-value is
is a x-intercept, meaning it crosses the x-axis at this point. The y-value is
 ⇒
⇒
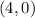 is the first point.
is the first point.
 is a y-intercept, meaning it crosses the y-axis at this point. The x-value is
is a y-intercept, meaning it crosses the y-axis at this point. The x-value is
 ⇒
⇒
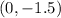 is the second point.
is the second point.
Now, plug these values into the point-slope formula:
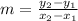

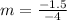

Plug this information into the equation to get your final answer of
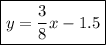 .
.