Answer:
Distance between balloon and a is = 383.67 m
Explanation:
The given situation can be represented as the given diagram as attached in the answer area.
cd = 384 m
cb = 200 m
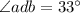
To find:
Distance between balloon and a i.e. side ad = ?
Solution:
First of all, let us consider the right angled
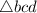 .
.
We know the trigonometric identity that:

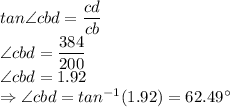
Now, using the external angle property for the external
 for the
for the
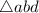 :
:
(External angle is equal to the sum of two opposite angles of the triangle.)
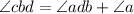

Now, let us consider the right angled
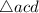 .
.
We have the value of
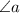 and perpendicular dc.
and perpendicular dc.
We have to find the hypotenuse ad.
Let us use the sine identity:

So, the answer is:
Distance between balloon and
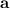 is = 383.67 m
is = 383.67 m