Answer:
A.

Explanation:
Given

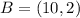
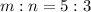
Required
Determine the coordinates of C
Since, point D divides line AB in ratio, 5 : 3;
We start by calculating the coordinates of D;
This is done as follows;
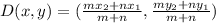
Where
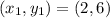
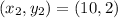
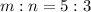
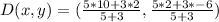
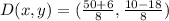
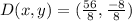
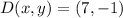
Since AC is vertical
Then, Point C has the same x coordinate as A
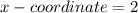
Similarly;
Since CD is horizontal
Then, Point C has the same y coordinate as D
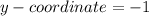
Hence,
