Question

Paige launched a ball using a catapult she built. The height of the ball (in meters above the ground) ttt seconds after launch is modeled by h(t)=-5t^2+40th(t)=−5t 2 +40th, left parenthesis, t, right parenthesis, equals, minus, 5, t, squared, plus, 40, t Paige wants to know when the ball will hit the ground. 1) Rewrite the function in a different form (factored or vertex) where the answer appears as a number in the equation. h(t)=h(t)=h, left parenthesis, t, right parenthesis, equals 2) How many seconds after launch does the ball hit the ground? seconds

Answer 1

-5t(t - 8) and it hit 8 seconds after launch.

Answer 2

1) Factor form :
`h(t)=-5t(t-8)`

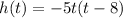
2) 8 second after launch.

Explanation:

The height of the ball (in meters above the ground) t seconds after launch is modeled by

`h(t)=-5t^2+40t`

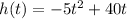
To find the time when ball hit the ground, we need to find the factor form of the given function.

`h(t)=-5t(t-8)`

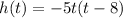
When ball hi the ground, then height of the ball from the ground is 0.

`h(t)=0`

`-5t(t-8)=0`

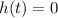
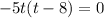
Using zero product property, we get

`-5t=0\Rightarrow t=0`

`t-8=0\Rightarrow t=8`

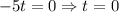
Ball hit the ground at t=0 and t=8. It means ball hit the ground in starting and 8 second after launch.