Answer:
The most appropriate value of the critical value is 2.289.
Explanation:
We are given that a researcher takes a random sample of 41 bulbs and determines that the mean consumption is 1.3 watts per hour with a standard deviation of 0.7.
We have to find that when constructing a 97% confidence interval, which would be the most appropriate value of the critical value.
Firstly, as we know that the test statistics that would be used here is t-test statistics because we don't know about the population standard deviation.
So, for finding the critical value we will look for t table at (41 - 1 = 40) degrees of freedom at the level of significance will be
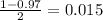 .
.
Now, as we can see that in the t table the critical values for P = 1.5% are not given, so we will interpolate between P = 2.5% and P = 1%, i.e;

So, the critical value at a 1.5% significance level is 2.289.