Question

A uniform stick 1.5 m long with a total mass of 250 g is pivoted at its center. A 3.3-g bullet is shot through the stick midway between the pivot and one end The bullet approaches at 250 m/s and leaves at 140 m/s

With what angular speed is the stick spinning after the collision?

Answer 1

63.44 rad/s

Step-by-step explanation:

mass of bullet = 3.3 g = 0.0033 kg

initial velocity of bullet
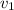`v_(1)` = 250 m/s

final velocity of bullet
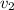`v_(2)` = 140 m/s

loss of kinetic energy of the bullet =
`(1)/(2)m(v^(2) _(1) - v^(2) _(2))`

==>
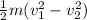
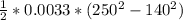`(1)/(2)*0.0033*(250^(2) - 140^(2) )` = 70.785 J

this energy is given to the stick

The stick has mass = 250 g =0.25 kg

its kinetic energy = 70.785 J

from

KE =
`(1)/(2) mv^(2)`

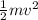
70.785 =
`(1)/(2)*0.25*v^(2)`

566.28 =
`v^(2)`

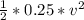
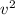
`v= √(566.28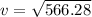)` = 23.79 m/s

the stick is 1.5 m long

this energy is impacted midway between the pivot and one end of the stick, which leaves it with a radius of 1.5/4 = 0.375 m

The angular speed will be

Ω = v/r = 23.79/0.375 = 63.44 rad/s