Question

The length of human pregnancies from conception to birth varies accordingly to a distribution that is approximately normal with mean 266 days and standard deviation 16 days. a study enrolls a random sample or 16 pregnant women. what are the mean and standard deviation of the sampling distribution of Xbar? What is the probability the average pregnancy length exceed 270 days?

Answer 1

The answer is below

Explanation:

Given that mean (μ) = 266 days, standard deviation (σ) = 16 days, sample size (n) = 16 women.

a) The mean of the sampling distribution of Xbar (
`\mu_x`) is given as:

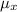`\mu_x=\mu=266\ days`

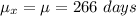
The standard deviation of the sampling distribution of Xbar (
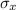`\sigma_x`) is given as:

`\sigma_x=(\sigma)/(√(n) ) =(16)/(√(16) )=4`

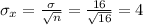
b) The z score is a measure in statistics used to determine by how much the raw score is above or below the mean. It is given by:

`z=(x-\mu)/(\sigma/√(n) )`

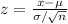
For x > 270 days:

`z=(x-\mu)/(\sigma/√(n) )=(270-266)/((16)/(√(4) ) )=1`

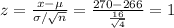
The probability the average pregnancy length exceed 270 days = P(x > 270) = P(z > 1) = 1 - P(z < 1) = 1 - 0.8413 = 0.1587 = 15.87%