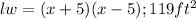Answer:
D.
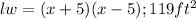
Explanation:
Dimensions of the old square brick patio:
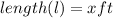
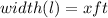
Note: a square has equal side measure
Dimensions of the new patio
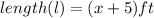 ==> she increased length by 5 ft
==> she increased length by 5 ft
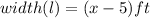 she reduced width by 5 ft
she reduced width by 5 ft
Expression of the length and width of the new patio is:

Area of the new patio:
Dimension of original patio = x by x = 12 ft by 12 ft.
To find area of the new patio, replace x with 12 in the expression,
 , which gives you the area.
, which gives you the area.
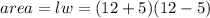

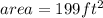
Answer is D.