Question

What is the equation of the line that is parallel to y = negative two-thirds x + 4 and that passes through (–2,–2)? On a coordinate plane, a line goes through (3, 2), and (6, 0). A point is at (negative 2, negative 2). y = negative two-thirds x minus four-thirds y = negative two-thirds x minus StartFraction 10 Over 3 EndFraction y = negative two-thirds x minus two-thirds y = negative two-thirds x minus StartFraction 17 Over 4 EndFraction

Answer 1

B.) y = negative two-thirds x minus StartFraction 10 Over 3 EndFraction

Explanation:

Answer 2

Option B.

Explanation:

If equation of a line is y=mx+c, then m is the slope of line.

The given equation is

`y=-(2)/(3)x+4`

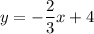
Here, slope of line is
`m=-(2)/(3)`.

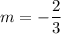We need to find the equation of line that is parallel to given equation and passes through (–2,–2).

We know that, slope of parallel lines are same. So, slope of required line is
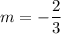`m=-(2)/(3)`. So, equation of line is

`y-y_1=m(x-x_1)`

`y-(-2)=-(2)/(3)(x-(-2))`

`3(y+2)=-2(x+2)`

`3y+6=-2x-4`

`3y=-2x-4-6`

`3y=-2x-10`

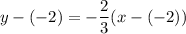
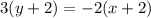
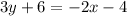
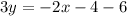
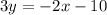
Divide both sides by 3.

`y=(-2x-10)/(3)`

`y=-(2)/(3)x-(10)/(3)`

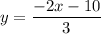
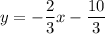
Therefore, the correct option is B.