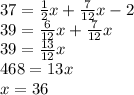Answer:
A
Explanation:
First, let's label the variables:
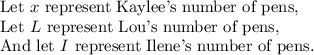
The first and second sentence, Kaylee at the start has x pens. She gave half to Lou, who started out with two fewer than Kaylee.
In other words, the total Lou now has is:
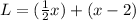
The first term represents what Kaylee gave to Lou. The second term represents what Lou had originally (two fewer than Kaylee [x]).
Simplifying, we get:
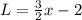
Third sentence. Lou give half of his new total to Ilene, who started out with three fewer pens than Lou. Lou, remember, started with three fewer than Kaylee (x-2). In other words:
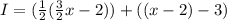
The left represents what is given to Ilene: one-third of Lou's new total. The right represents Ilene's original total: three fewer than Lou: or five fewer than Kaylee. Simplifying gives:
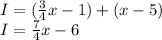
Finally, Ilene gives a third of this new amount to Kaylee, and Kaylee's final amount is 37. Thus:
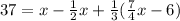
The first term represents what Kaylee originally started with. The second term represents what she gave to Lou. And the third term represents what Ilene gave to Kaylee. Simplify: