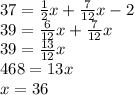Question

Help please!! Thanks

Answer 1

A

Explanation:

First, let's label the variables:

`\text{Let }x \text{ represent Kaylee's number of pens,}\\\text{Let }L \text{ represent Lou's number of pens,}\\\text{And let }I \text{ represent Ilene's number of pens.}`

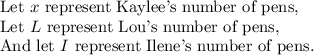
The first and second sentence, Kaylee at the start has x pens. She gave half to Lou, who started out with two fewer than Kaylee.

In other words, the total Lou now has is:

`L=((1)/(2)x )+(x-2)`

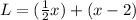
The first term represents what Kaylee gave to Lou. The second term represents what Lou had originally (two fewer than Kaylee [x]).

Simplifying, we get:

`L=(3)/(2)x-2`

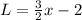
Third sentence. Lou give half of his new total to Ilene, who started out with three fewer pens than Lou. Lou, remember, started with three fewer than Kaylee (x-2). In other words:

`I=((1)/(2)((3)/(2)x-2) )+((x-2)-3)`

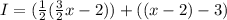
The left represents what is given to Ilene: one-third of Lou's new total. The right represents Ilene's original total: three fewer than Lou: or five fewer than Kaylee. Simplifying gives:

`I=((3)/(4) x-1)+(x-5)\\I=(7)/(4)x-6`

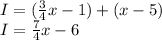
Finally, Ilene gives a third of this new amount to Kaylee, and Kaylee's final amount is 37. Thus:

`37=x-(1)/(2)x+(1)/(3)((7)/(4)x-6)`

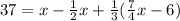
The first term represents what Kaylee originally started with. The second term represents what she gave to Lou. And the third term represents what Ilene gave to Kaylee. Simplify:

`37=(1)/(2)x+(7)/(12)x-2\\39=(6)/(12)x+(7)/(12)x \\39=(13)/(12)x\\ 468=13x\\x=36`