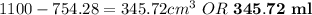Answer:
Volume left in the cylinder if all the cone is made full:
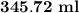
Explanation:
Given
Radius of cylinder = 5 cm
Height of cylinder = 14 cm
Radius of cone = 6 cm
Height of cone = 20 cm
To find:
Liquid remaining in the cylinder if cone is made full from cylinder's liquid.
Solution:
We need to find the volumes of both the containers and find their difference.
Volume of cylinder is given by:
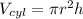
We have r = 5 cm and
h = 14 cm
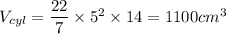
Volume of a cone is given by:
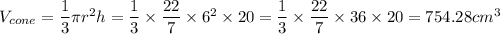
Volume left in the cylinder if all the cone is made full: