Answer:
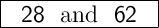
Explanation:
Hello, let's note a and b the two numbers.
We can write that
a = 6 + 2b
ab = 1736
So

We are looking for positive numbers so the solution is b = 28
and then a = 6 +2*28 = 62
Hope this helps.
Do not hesitate if you need further explanation.
Thank you