Question

Given: Circle k(O), diameter US , m RU=50°, m UT=30° Find: m∠RUS, m∠STU

Answer 1

`\boxed{m<RUS = 65 \ degrees}\\\boxed{m<STU = 90 \ degrees}`

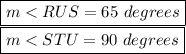
Explanation:

Finding m∠RUS:

Given that RU = 50°, So Central Angle ROU = 50° too because the measure of arc is equal to its central angle

Now, Let's assume a triangle ROU. It is an isosceles triangle since RO = RU (Radii of the same circle)

So,

∠ORU ≅ ∠OUR (Angles opposite to equal sides are equal)

So, we can write them as 2(∠RUO)

So,

2(∠RUO)+50 = 180 (Interior angles of a triangle add up to 180)

2(∠RUO) = 180-50

2(∠RUO) = 130

Dividing both sides by 2

∠RUO = 130/2

∠RUO = 65 degrees

m∠RUS = 65 degrees (Both are the same)

Finding m∠STU now:

In a semi circle (Given that SU is a diameter) , there must be a 90 degrees angle sin it opposite to the diameter.

So,

m∠STU = 90 degrees