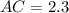Question

Given: ΔABC, AC = BC, AB = 3 CD ⊥ AB, CD = √3 Find: AC

Answer 1

`\boxed{2.29}`

Explanation:

The length of AB is 3 units.

The length of CD is
`√(3)` units.

D is the mid-point of points A and B.

AD is half of AB.

`(3)/(2) =1.5`

Apply Pythagorean theorem to solve for length of AC.

`c=√(a^2 +b^2 )`

The hypotenuse is length AC.

`c=\sqrt{1.5^2 +(√(3)) ^2 }`

`c=√(2.25+3 )`

`c=√(5.25)`

`c= 2.291288...`

Answer 2

`\boxed{AC = 2.3}`

Explanation:

AD = BD (CD bisects AB means that it divides the line into two equal parts)

So,

AD = BD = AB/2

So,

AD = 3/2

AD = 1.5

Now, Finding AC using Pythagorean Theorem:

`c^2 = a^2+b^2`

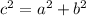
Where c is hypotenuse (AC), a is base (AD) and b is perpendicular (CD)

`AC^2= (1.5)^2+(√(3) )^2`

`AC^2 = 2.25 + 3`

`AC^2 = 5.25`

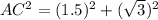
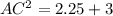
Taking sqrt on both sides

`AC = 2.3`