Question

what is the first step in writing f(x)=6x^2+5-42x in vertex form? a) factor 6 out of each term. b) factor 6 out of the first two terms. c) write the function in standard form. d) write the trinomial as a binomial squared.

Answer 1

C.) Write the function in standard form

Explanation:

Answer 2

Answer c): write the function in standard form

Explanation:

To start with, it is important to write the polynomial in standard form, so as to have the two terms with the dependence in x together:

`6x^2-42\,x+5`

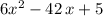
then you extract 6 as a common factor of just the terms with the variable x:

`6(x^2-7x)+5`

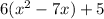
Then proceed to complete the square in the expression inside the parenthesis:

`6(x^2-7x+(49)/(4) -(49)/(4))+5`

`6\,((x-(7)/(2) )^2-(49)/(4) )+5\\6\,(x-(7)/(2) )^2-(147)/(2)+5\\6\,(x-(7)/(2) )^2-(137)/(2)`

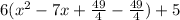
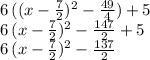
Then, the function can be finally be written as:

`f(x)=6\,(x-(7)/(2) )^2-(137)/(2)`

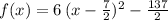
in vertex form