Question

Show that 3 · 4^n + 51 is divisible by 3 and 9 for all positive integers n.​

Answer 1

To prove that 3·4ⁿ + 51 is divisible by 3 and 9, we have;

3·4ⁿ is divisible by 3 and 51 is divisible by 3

Where we have;

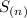`S_((n))` = 3·4ⁿ + 51

`S_((n+1))` = 3·4ⁿ⁺¹ + 51

`S_((n+1))` -
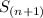`S_((n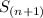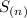))` = 3·4ⁿ⁺¹ + 51 - (3·4ⁿ + 51) = 3·4ⁿ⁺¹ - 3·4ⁿ

`S_((n+1))` -
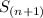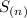`S_((n))` = 3( 4ⁿ⁺¹ - 4ⁿ) = 3×4ⁿ×(4 - 1) = 9×4ⁿ

∴
`S_((n+1))` -
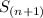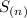`S_((n))` is divisible by 9

Given that we have for S₀ = 3×4⁰ + 51 = 63 = 9×7

∴ S₀ is divisible by 9

Since
`S_((n+1))` -
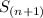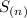`S_((n))` is divisible by 9, we have;

`S_((0+1))` -
`S_((0))` =
`S_((1))` -
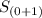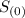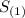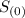`S_((0))` is divisible by 9

Therefore
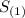`S_((1))` is divisible by 9 and
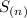`S_((n))` is divisible by 9 for all positive integers n

Explanation: