Question

Use the elimination method to solve the system of equations choose the correct ordered pair x-3y=-23 5x+6y=74

Answer 1

4,9

Explanation:

Answer 2

( 4, 9 ) is our solution in an ordered pair, as you could also say x = 4, and y = 9

Explanation:

So we have the following system of equations at hand ( given directly below ), and want to make it such that each equation is multiplied by a value that makes a common variable, say x, have opposite values of coefficients such that they cancel each other out when the two equations are added, enabling you to solve for the value of the other variable, in this case variable y.

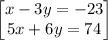`\begin{bmatrix}x-3y=-23\\ 5x+6y=74\end{bmatrix}` - Multiply this top equation by -5, so the coefficient of variable x becomes - 5, opposite to the respective x coefficient in the second equation.

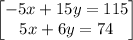`\begin{bmatrix}-5x+15y=115\\ 5x+6y=74\end{bmatrix}` - Adding the two equations we receive the simplified equation 21y = 189. y = 189 / 21 = 9. If y = 9, x should = - 23 + 3y = - 23 + 3
`*` 9 = 4. To get this value of x simply isolate the value of x in the first equation given to us, and substitute the known value of y. We have our solution in the form ( 4, 9 ), where x = 4 and y = 9.