Answer:
See Explanation
Explanation:
Given
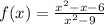
Required
Why is the function not continuous at x = 3
First substitute 3 for x at the denominator
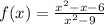
Factorize the numerator and the denominator
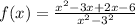
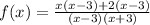

Divide the numerator and denominator by (x - 3)
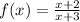
Substitute 3 for x
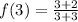
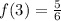
Because
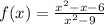 is defined when x = 3;
is defined when x = 3;
Then the function is continuous