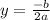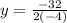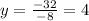Question

1. Identify the axis of symmetry for y = -3(x+3)^2-2. a. x = -2 b. x = 3 c. x = 2 d. x = -3 2. Choose the correct axis of symmetry for x = -4(y -4)^2+6 a. y = -6 b. y = -4 c. y =6 d. y = 4

Answer 1

`\boxed{x=-3} \\ \boxed{y=4}`

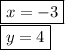
Explanation:

Axis of symmetry is a line that cuts the parabola in half touching the vertex.

Quadratic forms ⇒ y = ax² + bx + c or x = ay² + by + c

Axis of symmetry ⇒ x =
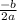`(-b)/(2a)` or y =
`(-b)/(2a)`

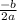
First problem:

y = -3(x+3)²-2

Write in quadratic form ⇒ y = ax² + bx + c

y = -3(x² + 6x + 9) - 2

y = -3x² -18x - 27 - 2

y = -3x² -18x - 29

a = -3, b = -18

Find axis of symmetry.

`x= (-b)/(2a)`

`x=(--18)/(2(-3))`

`x=(18)/(-6)=-3`

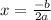
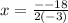
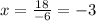
Second problem:

x = -4(y -4)² +6

Write in quadratic form ⇒ x = ay² + by + c

x = -4(y² - 18y + 16) + 6

x = -4y² + 32y - 64 + 6

x = -4y² + 32y - 58

a = -4, b = 32

Find axis of symmetry.

`y= (-b)/(2a)`

`y=(-32)/(2(-4))`

`y=(-32)/(-8)=4`

Answer 2

The answer is :

1. D
2. D

Explanation:

Axis of symmetry is the equation where it cuts the middle of the quadratic graph.

For quadratic equation in the form of (x+a)² + b, the axis of symmetry will be (x+a) = 0 which is x = -a :

Question 1,

`(x + 3) = 0`

`x = - 3`

Question 2,

`(y - 4 )= 0`

`y = 4`