Question

When the current in a toroidal solenoid is changing at a rate of 0.0260 A/s, the magnitude of the induced emf is 12.2 mV. When the current equals 1.40 A, the average flux through each turn of the solenoid is 0.00308 Wb. How many turns does the solenoid have?

Answer 1

The solenoid has 213 turns.

Step-by-step explanation:

The number of the solenoid's turns (N) can be found as follows:

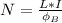`N = (L*I)/(\phi_(B))` (1)

Where:

L: is the self-inductance of the solenoid

I: is the current = 1.40 A

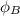`\phi_(B)`: is the magnetic flux = 0.00308 Wb

The self-inductance of the solenoid (L) is:

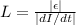`L = (|\epsilon|)/(|dI/dt|)` (2)

Where:

ε: is the induced emf = 12.2x10⁻³ V

dI/dt: is the rate changing of the current = 0.0260 A/s

By entering equation (2) into (1) we can find the number of turns:

`N = (|\epsilon|*I)/(\phi_(B)|dI/dt|) = (12.2 \cdot 10^(-3) V*1.40 A)/(0.00308 Wb*0.0260 A/s) = 213`

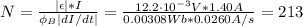
Therefore, the solenoid has 213 turns.

I hope it helps you!