Question

Recall the scenario about Eric's weekly wages in the lesson practice section. Eric's boss have been very impressed with his work. He has given him a $2 raise and now Eric earns $12 an hour. His boss also has increased Eric's hours to 10 to 25 hours per week. The restrictions remain the same; he needs to work a full-hour in order to get the hourly wage working 1.5 hour does not pay him for 1.5 hours but for one hour. Tasks: Consider the scenario and restrictions and interpret the work hour and potential earning relation as a function. Express the relation in the following formats: 1. Function equation 2. Domain of the function in the set notation (Would domain (work hours) be infinite?(write the domain in the set notation) 3. Range of the function in the set notation (Would the range (weekly wage) be infinite(write the range in the set notation) 4. Sketch the function and plot the points for his earnings.

Answer 1

`1)\quad f(x)=\bigg\{\begin{array}{ll}12x&0\leq x <9\\18x-48&9\leq x \leq 24\end{array}`

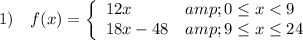
2) D: x = [0, 24]

3) R: y = [0, 384]

4) see graph

Explanation:

Eric's regular wage is $12 per hour for all hours less than 9 hours.

The minimum number of hours Eric can work each day is 0.

f(x) = 12x for 0 ≤ x < 9

Eric's overtime wage is $18 per hour for 9 hours and greater.

The maximum number of hours Eric can work each day is 24 (because there are only 24 hours in a day).

f(x) = 18(x - 8) + 12(8)

= 18x - 144 + 96

= 18x - 48 for 9 ≤ x ≤ 24

The daily wage where x represents the number of hours worked can be displayed in function format as follows:

`f(x)=\bigg\{\begin{array}{ll}12x&0\leq x <9\\18x-48&9\leq x \leq 24\end{array}`

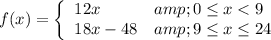
2) Domain represents the x-values (number of hours Eric can work).

The minimum hours he can work in one day is 0 and the maximum he can work in one day is 24.

D: 0 ≤ x ≤ 24 → D: x = [0, 24]

3) Range represents the y-values (wage Eric will earn).

Eric's wage depends on the number of hours he works. Use the Domain (given above) to find the wage.

The minimum hours he can work in one day is 0.

f(x) = 12x

f(0) = 12(0)

= 0

The maximum hours he can work in one day is 24 (although unlikely, it is theoretically possible).

f(x) = 18x - 48

f(24) = 18(24) - 48

= 432 - 48

= 384

D: 0 ≤ y ≤ 384 → D: x = [0, 384]

4) see graph.

Notice that there is an open dot at x = 9 for f(x) = 12x

and a closed dot at x = 9 for f(x) = 18x - 48