All three lines are parallel to each other.
To determine whether two lines are parallel, perpendicular, or neither, we can examine the slopes of the lines.
The general form of a linear equation is , where
 where is the slope and b is the y-intercept.
where is the slope and b is the y-intercept.
Let's compare the slopes of the given lines:
Line 1:
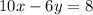
Rewrite it in slope-intercept form
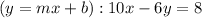
⟹
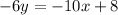
⟹
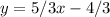
The slope of Line 1 is m₁ = 5/3.
Line 2:
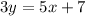
Rewrite it in slope-intercept form
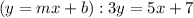
⟹
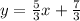
The slope of Line 2 is m₂ = 5/3.
Line 3:
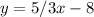
The slope of Line 3 is m₃ = 5/3.
Since m₁ = m₂, Lines 1 and 2 are parallel.
Since m₁ = m₃, Lines 1 and 3 are parallel.
Therefore, Lines 1, 2, and 3 are all parallel to each other.