Question

You are dealt two card successively without replacement from a shuffled deck of 52 playing cards. Find the probability that the first card is a king and the second is a queen. Round to nearest thousandth

Answer 1

0.078

Explanation:

The probability P(A) of an event A happening is given by;

P(A) =
`(number-of-possible-outcomes-of-event-A)/(total-number-of-sample-space)`

From the question;

There are two events;

(i) Drawing a first card which is a king: Let the event be X. The probability is given by;

P(X) =
`(number-of-possible-outcomes-of-event-X)/(total-number-of-sample-space)`

Since there are 4 king cards in the pack, the number of possible outcomes of event X = 4.

Also, the total number of sample space = 52, since there are 52 cards in total.

P(X) =
`(4)/(52)` =
`(1)/(13)`

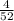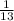
(ii) Drawing a second card which is a queen: Let the event be Y. The probability is given by;

P(Y) =
`(number-of-possible-outcomes-of-event-Y)/(total-number-of-sample-space)`

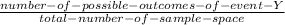
Since there are 4 queen cards in the pack, the number of possible outcomes of event Y = 4

But then, the total number of sample = 51, since there 52 cards in total and a king card has been removed without replacement.

P(Y) =
`(4)/(51)`

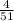
Therefore, the probability of selecting a first card as king and a second card as queen is;

P(X and Y) = P(X) x P(Y)

=
`(1)/(13) * (4)/(51)` = 0.078

Therefore the probability is 0.078