Answer:
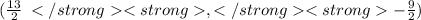
Explanation:

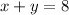
Solve the equation for y by moving 'x' to R.H.S and changing its sign

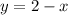
Substitute the given value of y into the equation 5x + y = 28
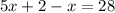
Solve the equation for x
Collect like terms
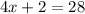
Move constant to R.H.S and change its sign
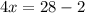
Subtract the numbers

Divide both sides of the equation by 4
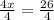
Calculate
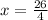
Reduce the numbers with 2
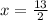
Now, substitute the given value of x into the equation y = 2 - x
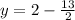
Solve the equation for y
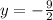
The possible solution of the system is the ordered pair ( x , y )

-------------------------------------------------------------
Let's check if the given ordered pair is the solution of the system of equation:
plug the value of x and y in both equation

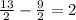
Simplify the equalities
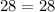
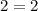
Since , all of the equalities are true, the ordered pair is the solution of the system.

Hope this helps....
Best regards!!