Question

Consider the following equation. x^2 - 4 x - 1 = 0 To complete the square, first rewrite the equation as x^2 - 4 x = 1. What value would then be added to both sides of the equation to complete the square? (Enter an exact number.)

Answer 1

`\large \boxed{\sf \ \ \ 4 \ \ \ }`

Explanation:

Hello, please find below my work.

`x^2-4x-1=0 \ \ \text{add 1 to both parts of the equation}\\\\<=> x^2-4x-1+1=0+1=1\\\\<=> x^2-4x=1`

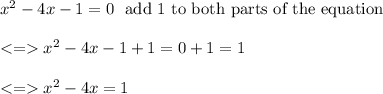
We know that for any a and x real numbers we can write

`(x-a)^2=x^2-2ax+a^2`

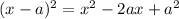
When we compare with the left part of the equation we can identify the term in x so that -4=-2a (multiply by -1) <=>4=2a (divide by 2) <=> a = 4/2 = 2

So we can write

`(x-2)^2=x^2-4x+2^2=x^2-4x+4`

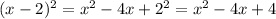
So we have to add 4 to both sides of the equation to complete the square and it comes:

`x^2-4x-1=0 \ \ \text{add 1 to both parts of the equation}\\\\<=> x^2-4x-1+1=0+1=1\\\\<=> x^2-4x=1 \ \boxed{\text{ add 4 to complete the square}} \\\\<=>x^2-4x\boxed{+4}=1+4=5\\\\<=>(x-2)^2=5 \ \text{ we take the root } \\ \\ <=>x-2=\pm √(5)\ \text{ we add 2 } \\ \\ <=> x = 2+√(5) \ \text{ or } \ x = 2-√(5)`

Hope this helps.

Do not hesitate if you need further explanation.

Thank you