Question

A small still is separating propane and butane at 135 °C, and initially contains 10 kg moles of a mixture whose composition is x = 0.3 (x = mole fraction butane). Additional mixture (x = 0.3) is fed at the rate of 5 kg mole/hr. The total volume of the liquid in the still is constant, and the concentration of the vapor from the still (xp) is related to x, as follows: Xp = How long will it take for X, to change from 0.3 to 0.35.​

Answer 1

Hello the needed relation is missing below is the required relation

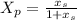`X_(p) = (x_(s) )/(1+x_(s) )` composition : propane = 0.70, butane = 0.3

Answer : ≈ 5.75 hrs

Step-by-step explanation:

Applying the data given in regards to the material balance

Butane balance input into the still = 5 mole feed/hr | 0.30 mol butane/molfeed

since the total volume of the liquid in the still is constant

The output from the still is = 5mol condensed/hr | x
`_(p)` mol butane/mol condensed

unsteady state equation =
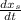`(dx_(s) )/(dt)` = 0.15 -
`0.5X_(p)`

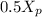
note : to reduce the equation a single dependent variable we have to substitute for
`x_(p)`

`(dx_(s) )/(dt)`
`= 0.15 + x_(s) / 1 + (0.5)x_(s)`

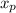
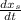
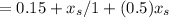
In order to find the time it will take for X to change from 0.3 to 0.35

integrate the above equation using the limits : t = 0, x
`_(s)` = 0.3 and t = Ф,

x
`_(s) = 0.35`

=
`[ - (x_(s) /0.35 - (1/(0.35)^2)* In(0.15 - 0.35x_(s) ) ]_(0.3) ^(0.35)`

hence t = Ф ≈ 5.75 hrs