Answer:
A real root of fifth-grade multiplicity/No complex roots.
Explanation:
The Fundamental Theorem of Algebra states that every polynomial with real coefficients and a grade greater than zero has at least a real root. Let be
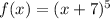 , if such expression is equalized to zero and handled algebraically:
, if such expression is equalized to zero and handled algebraically:
1)
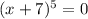 Given.
Given.
2)
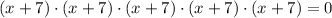 Definition of power.
Definition of power.
3)
 Given.
Given.
4)
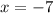 Compatibility with the addition/Existence of the additive inverse/Modulative property/Result.
Compatibility with the addition/Existence of the additive inverse/Modulative property/Result.
This expression has a real root of fifth-grade multiplicity. No complex roots.