Answer:
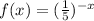
Explanation:
Given
The graph above
Required
Determine from the list of options, the function of the graph
To determine the function, we have to test each of the options
But first, we nees to write out the points on the graph
(1,5), (0,1), (-1,1/5) and (-2, 1/25)
A.

Point 1: When x = 1, f(x) = 5

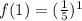
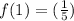
There's no need to check further as the first point doesn't lie on the graph
B.
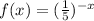
Point 1: When x = 1, f(x) = 5
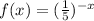
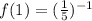
 --- Law of indices
--- Law of indices
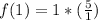
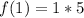
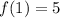
Point 2: When x = 0, f(x) = 1
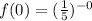
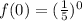
 --- The expression raise to power 0 is 1
--- The expression raise to power 0 is 1
Point 3: When x = -1, x = 1/5
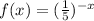

 ----- Law of indices
----- Law of indices
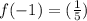
Point 4: When x = -2, x = 1/25
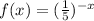

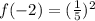 ----- Law of indices
----- Law of indices
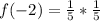
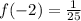
There's no need to check other options as this function satisfy the 4 points on the graph;
Hence;
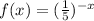 is the exponential function represented on the graph
is the exponential function represented on the graph