Question

Solve
5/x+y - 2/x-y = -1 and 15/x+y + 7/x-y = 10
Using cross-multiplication method.

Answer 1

x = 3 and y = 2

Explanation:

Start by multiplying the first equation by "-3" so we can cancel the term with denominator (x+y) when we combine:

`((-3)\,5)/(x+y) -((-3)\,2)/(x-y) =(-3)(-1)\\(-15)/(x+y) +(6)/(x-y) =3`

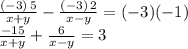
which now added term by term to the second equation gives:

`(-15)/(x+y) +(6)/(x-y) =3\\(15)/(x+y) +(7)/(x-y) =10\\ \\(13)/(x-y) =13`

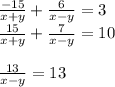
Now we solve for x-y by cross multiplying:

`(13)/(13)=x-y\\ x-y=1\\x=y+1`

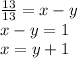
Now we use this substitution for x back in the first equation to solve for the unknown y:

`(5)/((y+1)+y) -(2)/((y+1)-y) =-1\\(5)/(2y+1) -2=-1\\(5)/(2y+1)=1\\5=2y+1\\4=2y\\y=2`

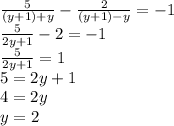
and now that we know that y = 2, we use the substitution equation to solve for x:

`x=y+1\\x=2+1\\x=3`