Question

Triangle A"B"C" is formed using the translation (x + 2 y + 0) and the dilation by a scale factor of from the origin. Which equation explains the relationship between AB and A"B"?

Answer 1

What The Other Guy Said Was Correct

Explanation:

2 + 2 = 4

Answer 2

segment a double prime b double prime = segment ab over 2

Explanation:

Triangle A″B″C″ is formed using the translation (x + 2, y + 0) and the dilation by a scale factor of one half from the origin. which equation explains the relationship between segment ab and segment a double prime b double prime?

coordinate plane with triangle ABC at A (- 3, 3), B (1, - 3), and C (- 3, -3).

segment a double prime b double prime = segment ab over 2

segment ab = segment a double prime b double prime over 2

segment ab over segment a double prime b double prime = one half

segment a double prime b double prime over segment ab = 2

Answer: If triangle ABC at A (- 3, 3), B (1, - 3), and c (- 3, -3) is translated using (x + 2, y + 0), then the new coordinates of triangle ABC would be at A'(- 3 + 2, 3), B'(1 + 2, - 3), and C'(- 3 + 2, -3) Which is A'(- 1, 3), B'(3, - 3), and C'(- 1, -3). The dilation by a scale factor of from the origin gives A″ (-1/2, 3/2), B″ (3/2, -3/2) and C″(-1/2, -3/2) = (-0.5, 1.5), B″ (1.5, -1.5) and C″(-0.5, -1.5)

The distance AB and A"B" are given as:

`AB=√((1-(-3))^2+(-3-3)^2) =√(5 2) \\\\A`

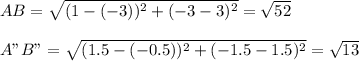
AB = √52 = √(4×52) = 2√13 = 2A"B"

A"B" = AB/2