Question

Two parallel wires run in a north-south direction. The eastern wire carries 15.0 A northward while the western wire carries 6.0 A northward. If the wires are separated by 30 cm, what is the magnetic field magnitude and direction at a point between the wires at a distance of 10 cm from the western wire?

Answer 1

The magnitude and direction of the magnetic field is 2.7 x 10⁻⁵ T upwards

Step-by-step explanation:

Given;

current in the eastern wire,
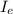`I_e` = 15 A

current in the western wire,
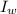`I_w` = 6 A

distance between the wires, d = 30 cm = 0.3 m

The magnetic field at a distance R from a line current I, is given as;

`B = (\mu_o I )/(2 \pi R)`

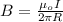
The magnetic field between the wires, are in opposite directions, and since the currents are also in opposite directions, the magnetic fields of the wires will be added.

The total field = magnetic field (east) + magnetic field (west);

`B = (\mu_o I_e)/(2 \pi R_e) + (\mu_0 I_w)/(2 \pi R_w) \\\\B = (\mu_o)/(2\pi) ((I_e)/(R_e) + (I_w)/(R_w))`

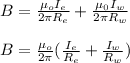
where;

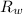`R_w` is the distance of the field from west = 10cm = 0.1 m

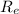`R_e` is the distance of the field on east from west = d - 10cm = 30cm - 10cm = 20cm = 0.2 m

The total magnetic field is;

`B = (\mu_o)/(2\pi) ((I_e)/(R_e) + (I_w)/(R_w))\\\\B = (4\pi *10^(-7))/(2\pi) ((15)/(0.2) + (6)/(0.1))\\\\B = 2*10^(-7)(75 + 60)\\\\B = 2*10^(-7)(135)\\\\B = 2.7*10^(-5) \ T`

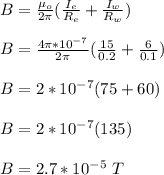
Since total magnetic field is positive, the direction of the field is upwards (positive y direction)

Therefore, the magnitude and direction of the magnetic field is 2.7 x 10⁻⁵ T upwards