Answer:
6 units
Explanation:
Let, Radius = r units
Height ( h ) = 3r units
Volume ( V ) = 24π units³
Now,
Let's find the height of the cylinder:
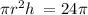
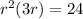
Calculate the product
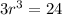
Divide both sides of equation by 3
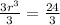
Calculate
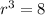
Write the number in the exponential form with an exponent of 3
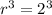
Take the root of both sides of the equation
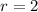
Replacing value,
Height = 3r
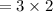
Calculate
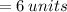
Hope this helps..
Best regards!!