Answer:
1) y=⅚x -2⅓
2) y=8/3x -5
Explanation:
Point-slope form:
y=mx+c, where m is the gradient and c is the y-intercept.
Parallel lines have the same gradient.
Gradient of given line=

Thus, m=⅚
Susbt. m=⅚ into the equation,
y= ⅚x +c
Since the line passes through the point (4, 1), (4, 1) must satisfy the equation. Thus, substitute (4, 1) into the equation to find c.
When x=4, y=1,
1= ⅚(4) +c
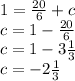
Thus the equation of the line is
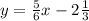 .
.
The gradients of perpendicular lines= -1.
Gradient of given line= -⅜
-⅜(gradient of line)= -1
gradient of line
= -1 ÷ (-⅜)
= -1 ×(-8/3)
=
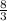
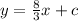
When x=3, y=3,
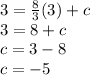
Thus the equation of the line is
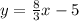 .
.