Question

Write the slip-intercept form of the equation of the line described

- through: (4,1), parallel to y = 5/6x - 3
- through: (3,3), perp. to y= -3/8x + 2

Answer 1

1) y=⅚x -2⅓

2) y=8/3x -5

Explanation:

Point-slope form:

y=mx+c, where m is the gradient and c is the y-intercept.

Parallel lines have the same gradient.

Gradient of given line=
`(5)/(6)`

Thus, m=⅚

Susbt. m=⅚ into the equation,

y= ⅚x +c

Since the line passes through the point (4, 1), (4, 1) must satisfy the equation. Thus, substitute (4, 1) into the equation to find c.

When x=4, y=1,

1= ⅚(4) +c

`1 = (20)/(6) + c \\ c = 1 - (20)/(6) \\ c = 1 - 3 (1)/(3) \\ c = - 2 (1)/(3)`

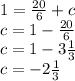
Thus the equation of the line is
`y = (5)/(6) x - 2 (1)/(3)`.

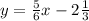The gradients of perpendicular lines= -1.

Gradient of given line= -⅜

-⅜(gradient of line)= -1

gradient of line

= -1 ÷ (-⅜)

= -1 ×(-8/3)

=
`(8)/(3)`

`y = (8)/(3) x + c`

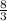
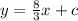
When x=3, y=3,

`3 = (8)/(3) (3) + c \\ 3 = 8 + c \\ c = 3 - 8 \\ c = - 5`

Thus the equation of the line is
`y = (8)/(3) x - 5`.