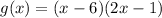Answer:
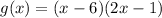
Explanation:
 intercepts the x-axis at these 2 points:
intercepts the x-axis at these 2 points:
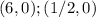
⇒ 6 and 1/2 are roots ie; if you insert
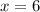 or
or
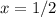 into the equation of g(x) you will obtain a 0.
into the equation of g(x) you will obtain a 0.
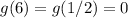
now in order for 0 to appear we should have
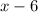
now in order for 0 to appear we should have
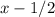
but
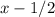 doesn't appear in any of these, but its multiple of 2 is there:
doesn't appear in any of these, but its multiple of 2 is there:
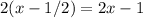
Therefore the function;