Answer: 0.49 ± 0.0237
Step-by-step explanation: A interval of a 99% confidence interval for the population proportion can be found by:
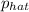 ± z.
± z.
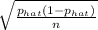
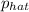 is the proportion:
is the proportion:
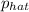 =
=
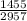
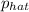 = 0.49
= 0.49
For a 99% confidence interval, z = 2.576:
0.49 ± 2.576.
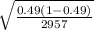
0.49 ± 2.576.
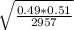
0.49 ± 2.576.(0.0092)
0.49 ± 0.0237
For a 99% confidence interval, the proportion will be between 0.4663 and 0.5137 or 0.49 ± 0.0237