Answer:
Adults Ticket = $18
Child's Ticket = $13
Explanation:
Let A denote the price of an adult's ticket
Let C denote the price of a child's ticket
It is given that the three adults and four children must pay $106.
Mathematically,
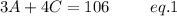
It is also given that the two adults and three children must pay $75.
Mathematically,
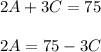
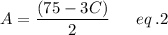
Substitute eq. 2 into eq. 1
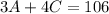
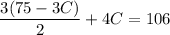
Simplify,
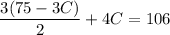
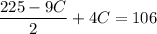
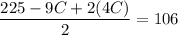

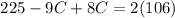
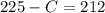
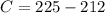
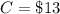
Substitute the value of C into eq. 2
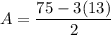
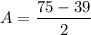
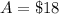
Therefore, the price of the adult's ticket is $18 and the price of a child's ticket is $13