Question

CAN ANYONE HELP ME PLEASE? Jen Butler has been pricing​ Speed-Pass train fares for a group trip to New York. Three adults and four children must pay $106. Two adults and three children must pay $75. Find the price of the​ adult's ticket and the price of a​ child's ticket.

Answer 1

adult=18$ and children=13$

Explanation:

a= adult. and. c= children

first change the statement into linear equation

3a+4c=106

2a+3c=75

then it just solving for a and y

3a+4c=106. a= 75-3c.

2

3(75-3c)+ 4c=106. solve for c

2

c=13

then find c by substituting the value you got into a . you can you either 3a+4c=106

or 2a+3c=75 to find the answer but the value of a is the same.

2a+3c=75. c=13

2a+3(13)=75

2a=75 -39

2a= 36

a=18

Answer 2

Adults Ticket = $18

Child's Ticket = $13

Explanation:

Let A denote the price of an adult's ticket

Let C denote the price of a child's ticket

It is given that the three adults and four children must pay $106.

Mathematically,

`3A + 4C = 106 \:\:\:\:\:\:\:\:\:\:\: eq. 1`

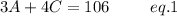
It is also given that the two adults and three children must pay $75.

Mathematically,

`2A + 3C = 75 \\\\2A = 75 - 3C`

`$ A = ((75 - 3C))/(2) \:\:\:\:\:\:\: eq\:. 2 $`

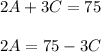
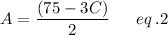
Substitute eq. 2 into eq. 1

`3A + 4C = 106`

`$ (3(75 - 3C))/(2) + 4C = 106 $`

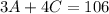
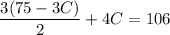
Simplify,

`$ (3(75 - 3C))/(2) + 4C = 106 $`

`$ (225 - 9C)/(2) + 4C = 106 $`

`$ (225 - 9C + 2(4C))/(2) = 106 $`

`$ (225 - 9C + 8C)/(2) = 106 $`

`$ 225 - 9C + 8C = 2(106) $`

`$ 225 - C = 212 $`

`C = 225 - 212`

`C = \$13`

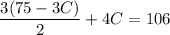
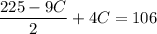
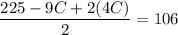
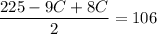
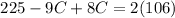
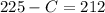
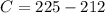
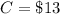
Substitute the value of C into eq. 2

`$ A = (75 - 3(13))/(2) $`

`$ A = (75 - 39)/(2) $`

`A = \$18`

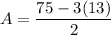
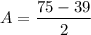
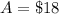
Therefore, the price of the​ adult's ticket is $18 and the price of a​ child's ticket is $13