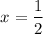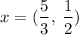Answer:
(A)
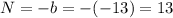
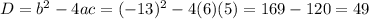
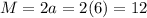
(B)
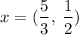
Explanation:
The given equation is
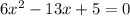
The solution is of the form as given by
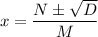
(A) Use the quadratic formula to solve this equation and find the appropriate integer values of N, M and D. Do not worry about simplifying the VD yet in this part of the problem.
The quadratic formula is given by
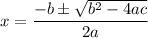
The equations of N, M and D are
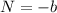
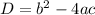
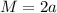
The values of a, b and c are
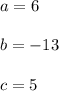
So,
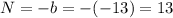
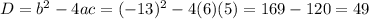
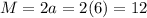
(B) Now simplify the radical and the resulting solutions. Enter your answers as a list of integers or reduced fractions, separated with commas. Example: -5/2-3/4
N = 13
D = 49
M = 12
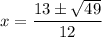
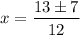
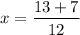 and
and
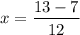
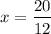 and
and
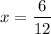
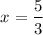 and
and