Answer:
C. 510 cm^2
Explanation:
Well to find TSA or Total Surface Area,
We need to find the area of al the triangles and rectangles.
Let's start with the 2 rectangles facing forwards.
They both have dimensions of 5*15 and 12*15,
75 + 180
= 255 cm ^2
Now let's do the back rectangle which has dimensions of 15 and 13.
15*13 = 195 cm^2
Now we can do the top and bottom triangles,
Since we don't have height we can use the following formula,
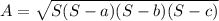
S is
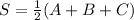
S= 15
Now with s we can plug that in,
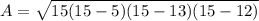
The a b and c are the sides of the triangle.
So let's solve,
15 - 5 = 10
15 - 13 = 2
15 - 12 = 3
10*2*3 = 60
60*15 = 900
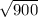 = 30 cm^2
= 30 cm^2
Since there is 2 triangles with the same dimensions their areas combined is 60 cm^2
60 + 255 + 195 = 510 cm^2
Thus,
the TSA of the right triangular prism is C. 510 cm^2.
Hope this helps :)